以下文章来源于力学人 ,作者力学家
超声导波检测技术是一种基于有界结构中低频应力波传播理论的无损检测技术,具有检测距离长、对人体无害、成本低的优点,被广泛应用于管道、钢轨、钢筋等细长结构的探伤中。然而,在利用超声导波检测远距离的小缺陷时,缺陷回波常表现为强噪声下的微弱信号特征,造成漏检风险。为了提高超声导波小缺陷的检测效率,本文基于双混沌系统构建了双混沌系统的弱信号定量检测理论,可同时识别缺陷回波的幅值和波到时刻,为缺陷的定量检测奠定了基础。该方法在机械系统早期故障诊断、地质勘探、雷达探测、生物信号检测、海洋探测等领域的弱信号检测中,具有十分重要的应用价值。
近日,东莞理工学院马宏伟教授团队在国际知名期刊Mechanical Systems and Signal Processing发表最新成果:Analysis and application of weak guided wave signal detection based on double Duffing oscillators,巧妙利用混沌系统的敏感性构造了双混沌检测系统,实现了弱超声导波信号的定量检测,该方法为弱导波信号的定量检测提供了理论基础。

超声导波检测技术是一种基于有界结构中低频应力波传播理论的无损检测技术,其具有检测距离长、速度快、成本低的优点,被广泛应用于管道、钢轨、钢筋等细长结构的探伤中。
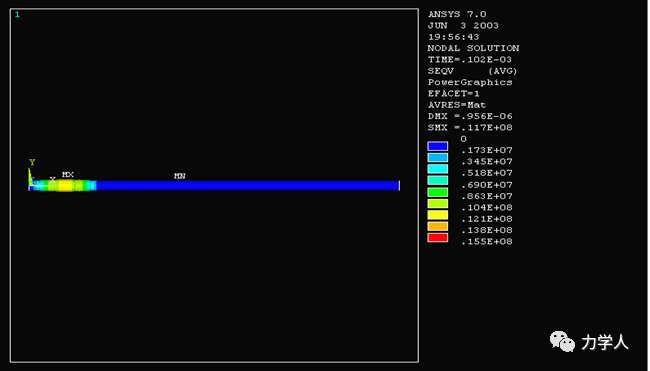
图1 超声导波检测结构缺陷示意图
在利用超声导波检测距离较长或缺陷较小时,缺陷回波将表现为强噪声下的弱信号,这给缺陷检测造成极大的挑战,易造成漏检、误检。常规的检测方法往往需要先消除噪声、再进行缺陷信号识别,在降噪处理中可能会对目标信号产生影响,进而无法准确识别缺陷参数。本方法直接利用混沌系统的敏感性、及其对噪声信号的免疫性实现了若导波信号的检测。考虑式(1)所示的Duffing方程,
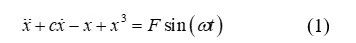
当给定阻尼系数c=0.4,ω=0.439823时,系统随驱动力F的分岔图,如图2所示。若设定F =0.457808为检测系统(系统处于周期态),则若在方程右侧叠加同频率的周期信号,就相当于增加了外驱动力F 的值,系统将突变为混沌态。研究表明,即便是F的幅值改变只有小数点后第6位有变化,系统状态都会有显著改变(从周期跳变为混沌),这就是混沌系统的敏感性。另一方面,这种敏感性只在待检信号与Duffing系统驱动力频率一致时才有效,如果噪声信号叠加到Duffing系统中,由于噪声信号的宽频特征,Duffing系统并不会发生突变。该方法正是利用这一原理实现强噪声下弱信号识别的。
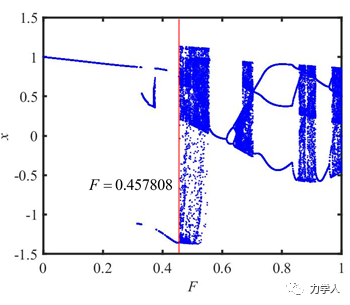
图2 Duffing方程随外驱动力F 的分岔图
通常情况下,采用Hanning窗调制的正弦信号激励超声导波,如图3所示为一典型的超声导波测试信号,图中三个波包分别为入射波、缺陷回波、端面回波。当缺陷较小或传播距离较长时,缺陷回波会变的十分微弱,如果在实际测试中还需要考虑噪声影响。
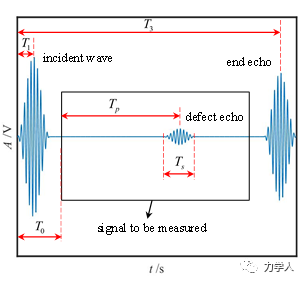
图3 典型的超声导波测试信号
截取入射波和端面回波之间的信号为待检信号,叠加到Duffing方程中,经推导(图4)可得Duffing方程驱动力幅值改变量ΔF将依赖于缺陷回波幅值A以及其发生时刻(通过叠加时产生的相位差影响)。

图4 导波信号对Duffing振子的影响规律研究
依据余弦函数关系式,对Duffing振子的驱动力项进行相位补偿,即在驱动力项上添加初相位以抵消相位差。当补偿相位和相位差2kπ时,ΔF取得最大值且就是导波幅值。据此,设计了算法流程(图5),将Duffing振子的参数调整到混沌临界状态作为检测系统1,将待测信号输入到系统1中,令补偿相位从0到2π逐渐增加,计算每一个补偿相位下Duffing系统的ΔF,获得ΔF与补偿相位之间的关系,其中ΔF的最大值即为导波幅值。
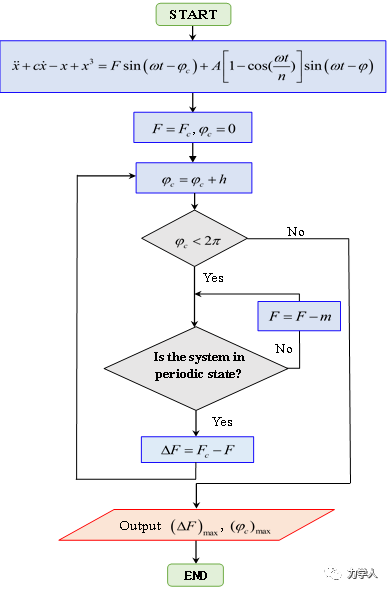
图5 基于Duffing振子相位补偿的算法流程图
生成三组信号,分别为导波信号、纯噪声、被噪声污染的导波信号(图6(a)-(c)),利用图5所示算法计算得到信号幅值(图6(d)-(f)),检测系统1准确地识别出了信号幅值,噪声的输入并未对系统幅值产生影响,表明系统对噪声具有免疫性。
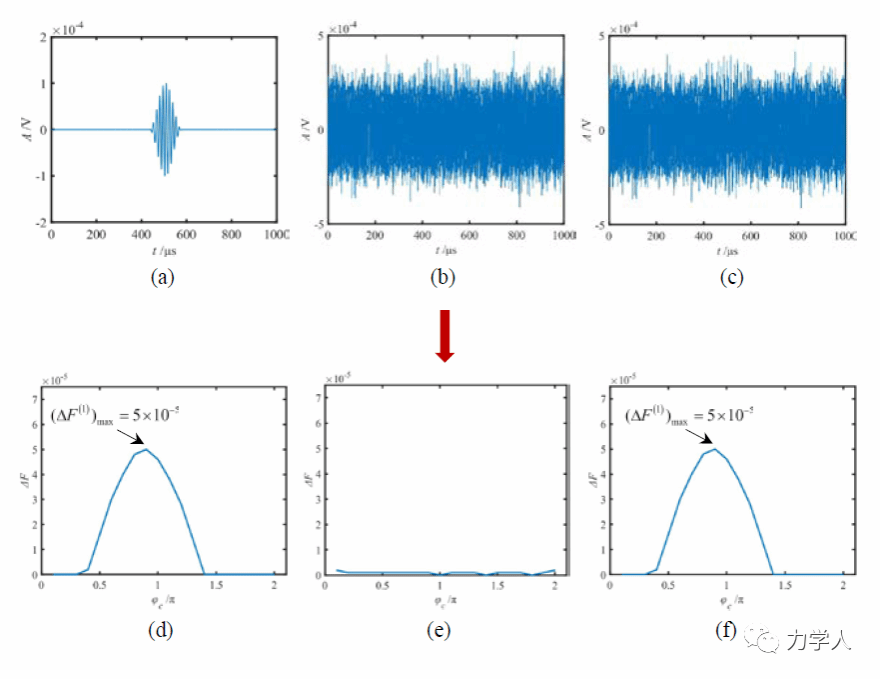
图6 仿真信号与幅值识别结果
进一步研究表明导波的峰值发生时刻Tp与相位差相关,这位识别信号发生时刻提供了思路。构造了与Duffing检测系统1满足一定频率关系的Duffing检测系统2,对两个系统的进行相位补偿,发现当两个系统的ΔF 达到最大值时,两个系统与信号是同相的,也即两个系统也是同相的。基于这一结论,结合Tp与相位差的关系,推导得到了利用补偿相位计算Tp的方法,具体过程见图7。

图7 导波信号波峰发生时刻计算方法研究
将模拟的纯导波、纯噪声、混有噪声的导波信号输入两个Duffing检测系统中,利用图5所示算法计算得到补偿相位(图8),计算波峰发生时刻Tp,相对误差为-2%,表明双Duffing系统可以从强噪声中准确识别信号发生时刻。
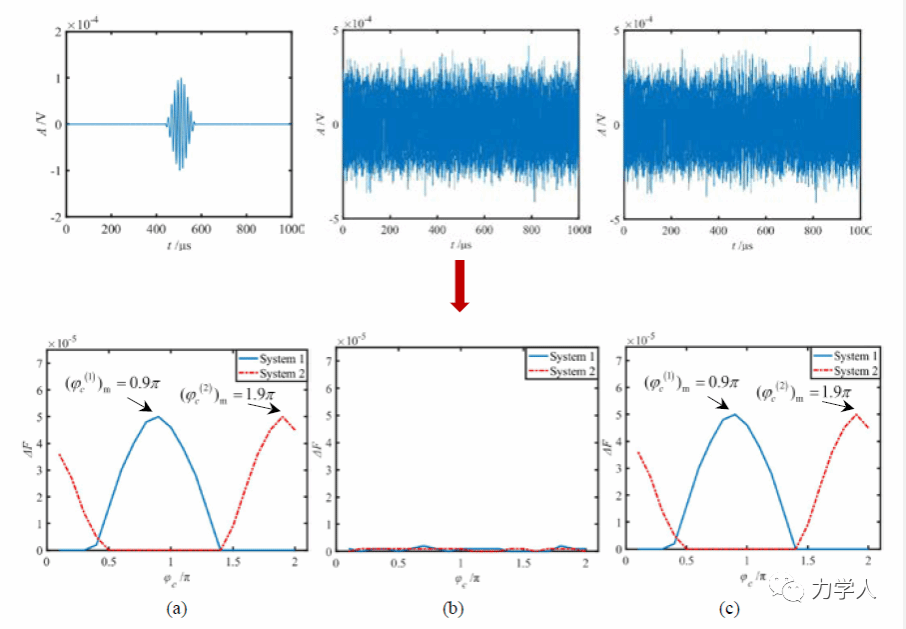
图8 补偿相位识别结果: (a) 导波信号; (b) 纯噪声; (c) 被噪声污染的导波信号
最后,为了验证所提方法的有效性,开展了超声导波检测管道小缺陷的实验研究(图9),并设置如图10所示5种分析工况。
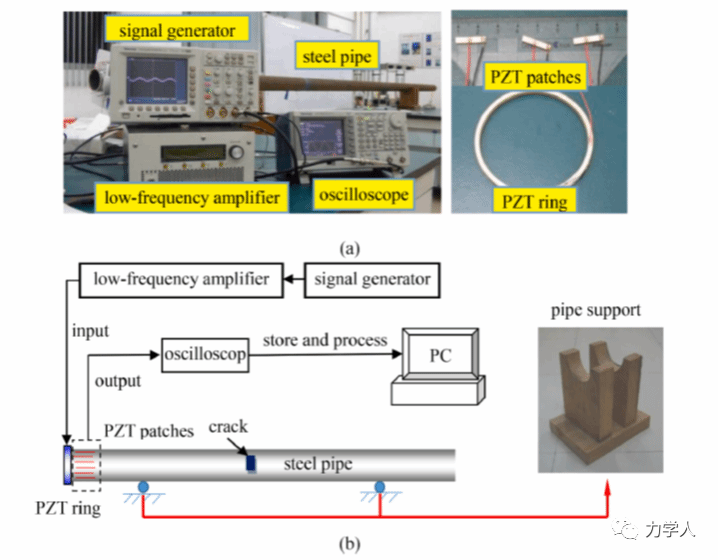
图9 超声导波检测管道实验方案
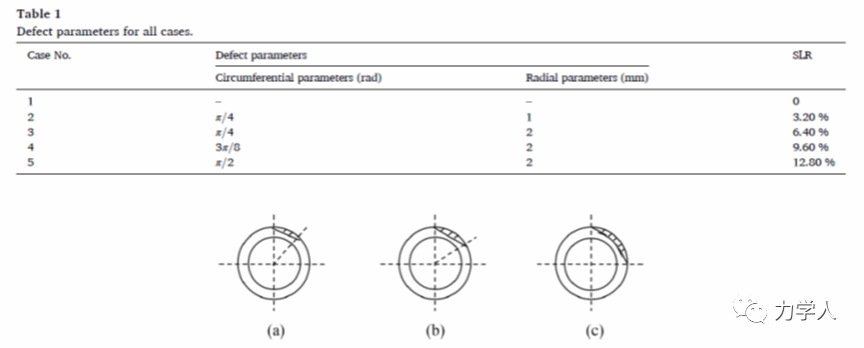
图10 5种工况的参数设置
将实验测试信号输入到双Duffing系统中,可以获得ΔF与补偿相位(图11),计算得到缺陷回波幅值与发生时刻,将这些参数与反射系数、波速信息结合,计算得到缺陷的尺寸与位置(表1,表2)。其中缺陷尺寸的识别相对误差不超过7%,位置识别相对误差不超过6%,这表明基于双Duffing振子的弱导波检测方法可以准确识别超声导波的幅值和发生时刻,有效提高超声导波检测技术在管道小缺陷检测中的灵敏度。这拓宽了超声导波检测技术的工程应用,发展了基于Duffing振子的弱信号检测方法,为管道的早期损伤识别提供了保证。
图11 测试信号与检测结果
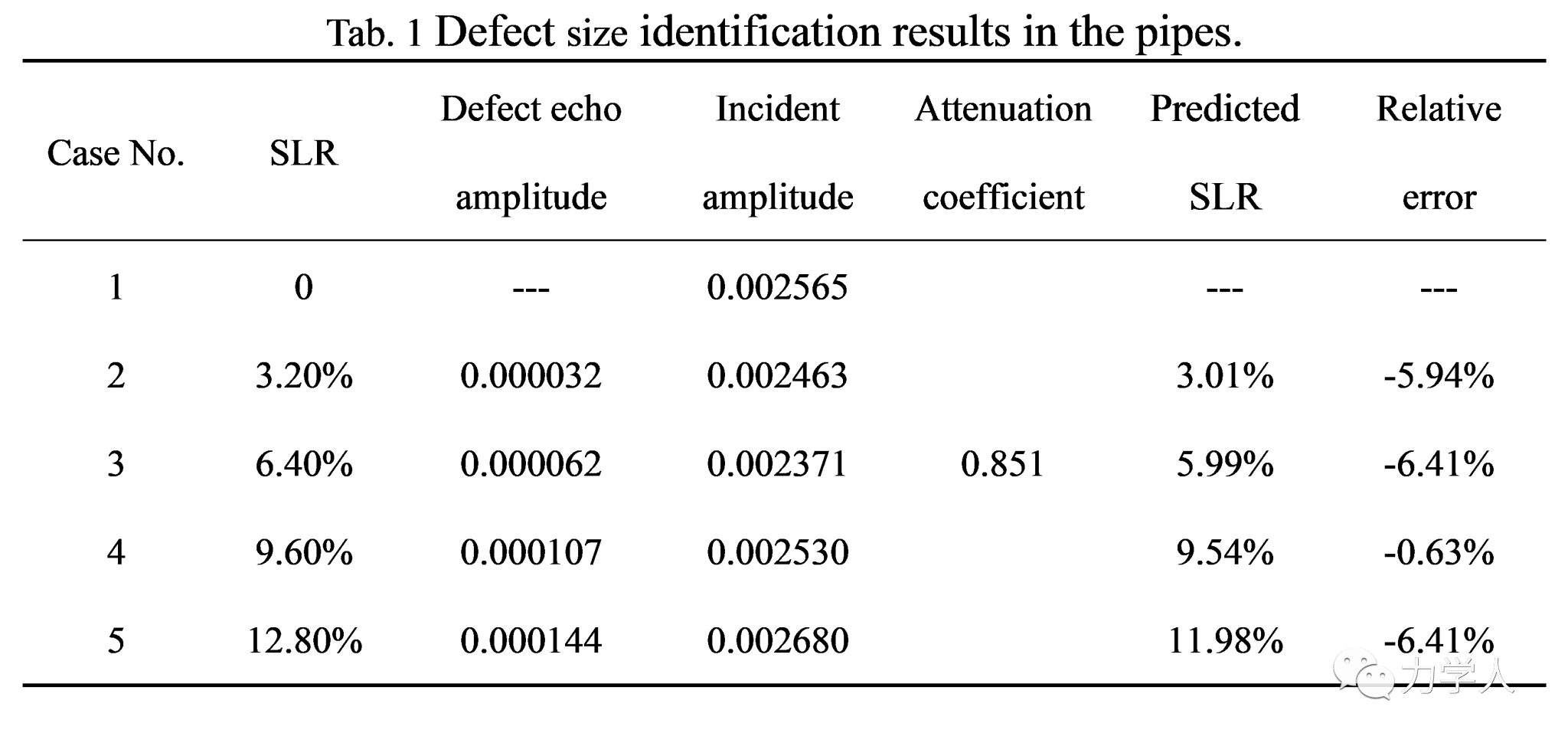
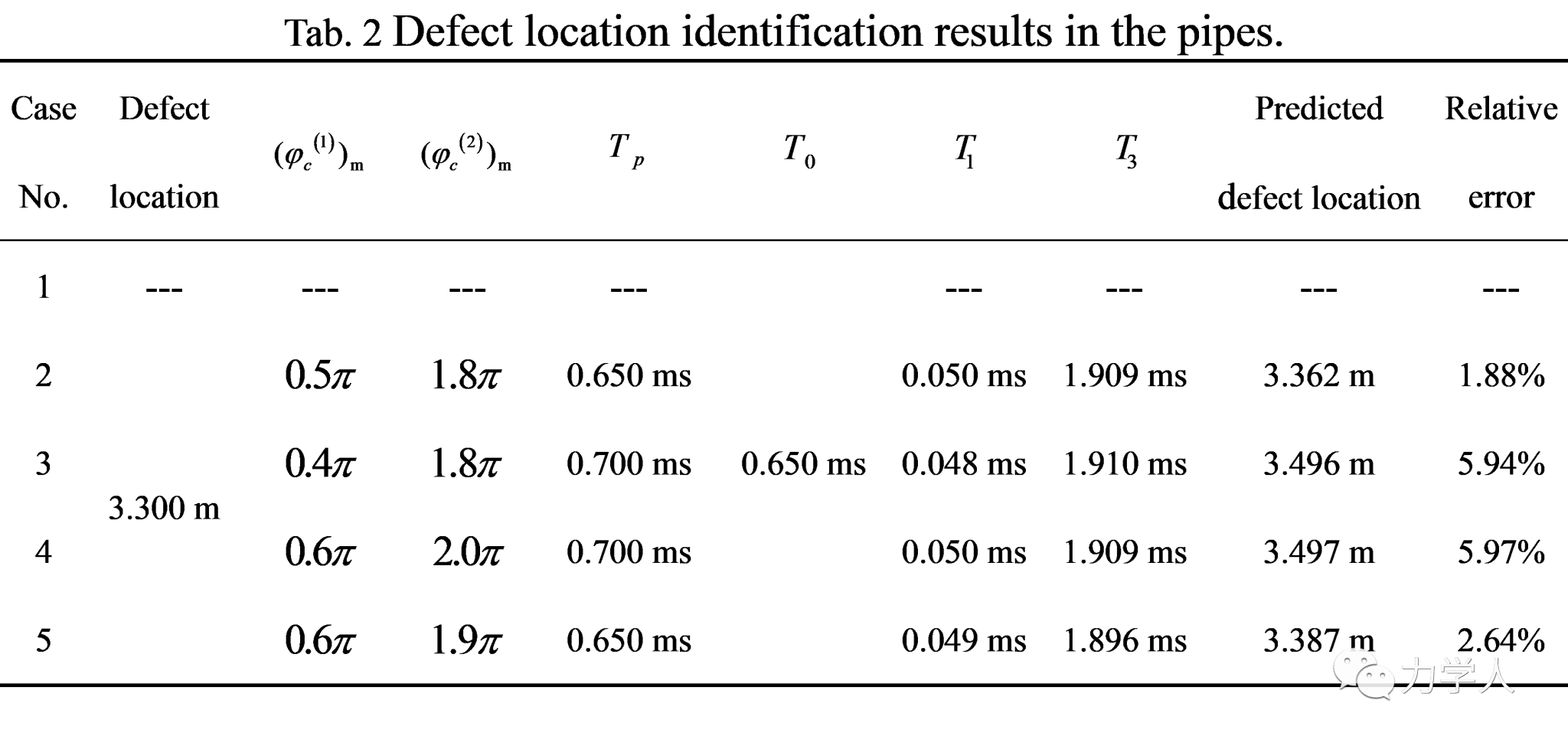
近年来,在机械系统早期故障诊断、地质勘探、雷达探测、生物信号检测、海洋探测等领域人们发现存在多种弱信号检测需求,为该方法的应用提供了广阔的领域。
暨南大学-东莞理工学院联合培养博士生成梦菲为论文第一作者,马宏伟教授、张伟伟教授为共同通讯作者,东莞理工学院机械学院老师武静为共同作者。该研究工作得到了国家自然科学基金、广东省普通高校机器人与智能装备重点实验室、东莞理工学院机器人与智能设备创新中心的资助。
原文链接:
https://doi.org/10.1016/j.ymssp.2023.110196

审核:力学家
力学类综合、全面、专业的信息平台,为力学发声。关注力学学科、力学与多学科交叉、力学工程应用领域的最新科研进展和资讯,坚持“前沿、探索、创新、引领、争鸣”的高精尖发展目标,为力学人搭建交流平台。欢迎关注,投稿联系:lxrgzh2021@163.com

免责声明:本公众号致力于打造专属力学人的交流平台,分享力学领域相关资讯,相关内容仅供参考学习,所有发表内容,均不代表【力学人】的观点。如若本公众号侵犯了媒体或个人的知识产权,我们将立即予以删除。
图文来源:马宏伟 聂振华教授课题组微信公众号

